In the Chapter 1 Tuples, Points and Vectors are covered. These are the building blocks for the rest of the TRTC. So lets start from the tuples.
Tuple is a data structure that contains ordered list of things. In our case these things are four Swift Floats. This is a quite a simple data structure but quoting to Jamis…
These tuples are going to be some of your ray tracer’s workhorses, so you’ll want them to be lean and fast! — Jamis Buck.
The four elements represents the coordinates (x, y, z, w). The first three are for the position in 3D space and the fourth is what separates points and vectors. For point w = 1 and for vector w = 0.
The great thing in the book is that all the test cases are predefined. This is really nice because you don’t have to figure out what numbers to use and what the test cases should return as output. You can focus on the actual testing and implementing. Test cases can be downloaded from the books website.
Testing
Writing a test follows a pattern where there are steps for Given, When and Then. You could read it like “Given values x when something happens with the value then it means this”. I’t will all become clear when we get to the code.
Is tuple a point or a vector and how the factory functions work?
Implementing tuple
Below is the implementation of the tuple struct. I followed here the books succession to desing functions that will create a point or a vector and functions to test if a tuple is a point or a vector respectively. The latter functionality could be paled inside the struct as a method but for now I will stick in the books scenario.
# Comparing the Floats #
There is a mention in the book that extra care must be given when comparing floating point values. I decided not to implement the actual comparing function here so I use the Swifts build in method for Floats.
Operations
Comparing tuples
A common thing that is often needed to know is if two tuples are equal. That’s what we test and implement here. This testing is mentioned in the book but there is no test scenario for this so this is kind of bonus case. This is a functionality we put in the tuple struct as a method. So this what the RGTuple look now.
This is how the RGTuple struct looks now after the isEqualTo method is implemented. The struct is still quite simple.
+ Add tuples +
We can’t add all kinds of tuples together or it doesn’t make sense to do so. The last w component defines what kind of a tuple the resulting tuple will be. Here are the listed cases:
- add point and vector => new point, w = 1
- add vector and vector => new vector, w = 0
add point and point => ?, w = 2
The test case in the book is written for point + vector case. I have also added the vector to vector case here for the completeness.
Implementing tuple adding I use operator overloading. Great tutorial about how to do operator overloading in Swift can be found in https://www.raywenderlich.com/2271-operator-overloading-in-swift-tutorial. In our case we must check that the tuples are the right type. If that is the case we do the actual adding and otherwise we just return the tuple that is on the left.
– Subtract tuples –
When subtracting there is also cases that makes sense and are useful and cases that don’t. Same idea is used in subtracting as in adding. Each matching component in the tuples is subtracted Here the cases are listed:
- subtract a point from point => vector, w = 0
- subtract a vector from point => newPoint, w = 1
- subtract a vector from vector => newVector
Operator overloading technique is also used to implement subtracting as it was used in adding. The code looks quite similar but the test are a bit different and obviously here we subtract the values instead of adding them.
Negating tuples
To know the opposite of the vector. This is important and often needed. Vectors are always from some x to y and when negating the vector you get from y to x. In the book there is a test case to negate vector by subtracting it from the (0, 0, 0, 0) vector. Since this is not the best solution I skip it here and use the second approach which is to just negate each of the components of the tuple. So this is the test case:
Implementing the negating functionality is really simple in Swift. We can use same kind of Swift operator overloading technique as with adding and subtracting. We only need to put word prefix in front of the func keyword. The code remains nice and short and we follow negation operator the book assumes. How ever I also added the negate() method in the RGTuple. Just for showing that it’s possible and it uses the Swift build in negate() method for Float that individual components uses.
* Multiply tuple by scalar *
What multiplying does to the vector is that it scales it by the magnitude of the scalar. To know the point that is 3.5 times farther than the original you just multiply every component in the vector. Test case is easy to follow.
Multiplication is as easy as it can be. Operator overloading is used here too.
/ Dividing tuple by scalar /
Multiply by 0.5 is equal to divide by 2. So as the book mentions there is this ability to implement division by multiplication. Here is the test case for dividing:
There is no mention in the book at this point about dividing by ZERO but I assume that I should add that check in my division implementation. Division also use the operator… 😉 you know.
Magnitude aka. length
Magnitude is calculated using the famous Pythagoras theorem where squares and square roots are taken. When vector magnitude is one 1, it is called unit vector. Obviously point don’t have any magnitude. Maybe someone who is really math oriented could argue that it have magnitude that is zero. So here are all five tests from the book:
Magnitude implementation is added in the RGTuple struct as a method since it’s quite natural place to put it. At this point the whole RGTuple struct looks like this:
Normalization
This is an important concept in graphics programming. Normalization means that the vector will be scaled to have magnitude of one.
ALERT!
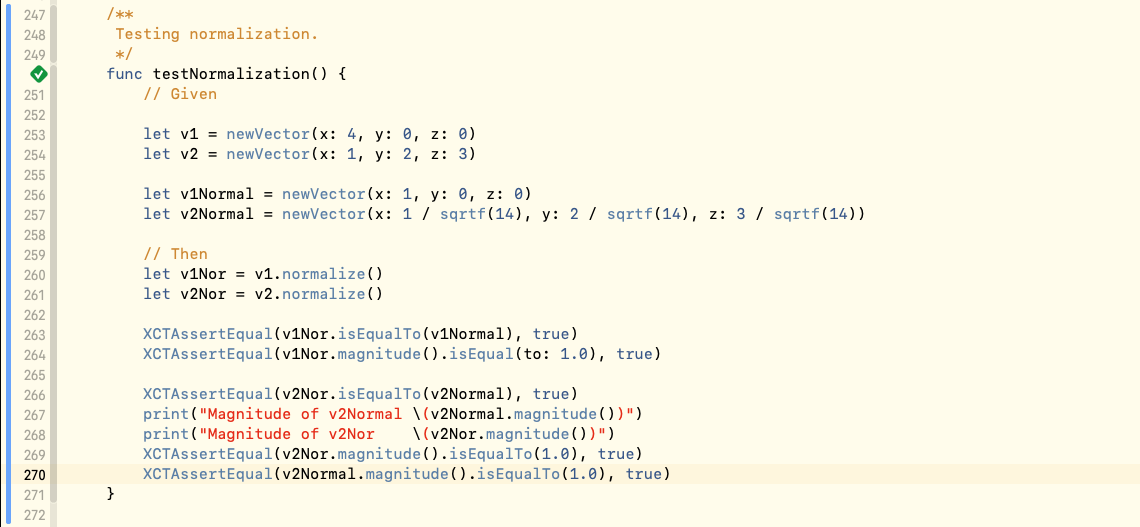
But wait! Here is a first problem that made me actually scratch my head. When testing the magnitude of normalized vector to one I got error on my test case. It could be seen below.

Now I must rewind a bit. There was this mention in the book about comparing floating point values. How important it is…and which I ignored. Reconsidering now 🙂
In this current test case the magnitude of the normalized vector v2 the v2Nor is 0.99999994 and when compared to 1.0 which should be the magnitude of normal vector there is an obvious gap. We can cleary see that these are not exactly equal.
In the picture above the v2Normal vector and the normalized v2 vector v2Nor are equal. So this is the test that succeed. But the magnitude of v2Nor is not 1.0. Neither is the magnitude of v2Normal equal to 1.0 since it’s the same 0.99999994 as it is for the v2Nor.
What we have here is the problem with the floating point precision when comparing them. In our case the Swift Float built-in isEqual method is too restrictive. Conclusion is that I must implement the equality method my self using the guide Jamis gave earlier. No easy way out I guess 😉
I decided to use Swift ability to extend existing data types using extensions. To keep the code base clean I put the Float extension(s) in a separate file. Below is the actual code for the extension.
To use the new method for Float the RGTuple needs a new equality testing method too. So here is how the implementation looks in the RGTuple struct.
Now the test cases that previously failed will succeed. Check out the image below.
Dot product – scalar product – inner product… you name it
Dot product takes two vectors and produces a scalar value. According to the example Jamis gives in his book the result of the dot product tells if the angle between the vectors is large or small. I dot product is 1 the vectors are identical and if its -1 they point to opposite directions. But my intension is not to stuck here in the details so here is the test case.
Implementing the dot product is simple. Read the Joe asks: – section in the book if you want to know why the w is included.
Cross product – “last one” 🙂
This differs from the dot product so that instead of producing a scalar the cross product produces another vector as result. So for example in the image above if you take X cross Y its Z. And if you take Y cross B you get -Z! First thing again is to write the test case. Here I have used an alternative way to initialise values in Swift.
Nothing too complex in the implementation.
So the Chapter 1 is done… well not just yet. There is this “Putting it together” section at the end of Chapter 1 where all the components done so far are used. I’m not going to go through this exercise here but there is a short example included in the Chapter 1 project folder. It’s implemented using Swift Playground. Using Playground is actually a quite handy in this case since you can visualise the movement of the projectile 🙂
Thanks for reading this far. Next chapter is coming soon.
